Abstractions as regularities in the world

Do abstractions exist? Here we go for the 641st time…

This piece is largely a response to silenceinbetween’s excellent post A Case For the Reality of Abstractions. (For brevity I will refer to the author as S going forward.)

S frames the problem as such:

The central tension here is that physics, as we currently understand it, operates like so: there was an initial set of conditions and laws which operate on those conditions. That’s it. That framework explains everything quantum, which explains everything atomic, which explains everything chemical, so on and so forth. Hence, anything “big” can be reduced to its parts and in fact everything “big” is just its parts. Abstractions are just illusions, then, maps we project onto reality. They aren’t real, can’t cause anything, do not exist.

So: do abstractions, like the number 4, exist? There are often two ways to answer this question:

• (1) No, the number 4 does not exist, not on its own. If you claim it exists, can you tell me where exactly it is? No, you can’t. Of course, we can use the label “4” to conveniently refer to things (“there are 4 apples in my basket”), but the number itself doesn’t exist anywhere we can point to in the world. It’s made up, it’s a construct of our imagination, much like Harry Potter or Santa Claus (sorry kids).
• (2) Yes, the number 4 does exist, you silly goose. Does something need to be located at a specific position in spacetime for us to claim that it exists? Wouldn’t you claim that justice exists, that aging exists? Is there one location in the world that you can point to and say: justice, it’s right here? No, you can’t. The number 4, like any other abstract entity, does exist, just not in any physical form: it exists in a separate realm of abstract entities.

For shorthand, let’s name these two groups the “pro-4” and the “anti-4” group. The pro-4 and anti-4 groups have a fundamental disagreement about ontology. Anti-4’s claim that only physical things exist, things that are made up of the basic building blocks of physics (particles, molecules, something something, I’m not a physicist), and Pro-4’s claim that in addition to physical things, there are non-physical things (ideas), and they have an existence of their own, independent of the physical world. Even before anyone had written down the number 4, even before there was four of anything in the universe, the number 4 still existed and continues to exist, in the timeless, spaceless world of abstractions.

So, who’s right? Well, let’s go back to S’s A Case For the Reality of Abstractions. S pulls a conceptual judo move that I find intriguing: they define an abstraction as a physical entity which, due to causal coupling, contains information about more than just itself.

Hold up though—an abstraction as a physical entity?! Sounds like a contradiction in terms. Abstractions are specifically supposed to be non-physical, right? But I think S is onto something. To build the intuition I’ll give an example, similar to the ones S gives in their post.

Imagine you have a giant pile of lego blocks in a bowl. It’s a big disordered mess. You shake up the bowl and all the pieces move into ‘random’ positions.

Don’t look too closely at the lego blocks…

Now, let’s say you wanted to track the positions of the lego pieces before and after you shake the bowl. Suppose you’ve measured the position of every piece before shaking, and you’ve given them all a label, e.g. one of the pieces is labelled Alfred, a red lego block.

Our friend Alfred

Now you shake the bowl, and you measure the position of Alfred. Does Alfred’s position tell you the position of all the other pieces after the shake-up? Well, it gives you some information, e.g. if Alfred is in position (X, Y, Z) you know that no other piece is in that position. But beyond that, you actually don’t know anything about the other pieces.¹

Now imagine that the bowl of lego blocks is not in a messy pile—they’re actually all stuck together into a big pyramid, and Alfred is the piece at one corner of the pyramid. You shake up the bowl again, and the pyramid hobbles around in the bowl. Now if you measure the position of Alfred, do you have information about the other pieces? Yes, now you actually know exactly where all the other pieces are!

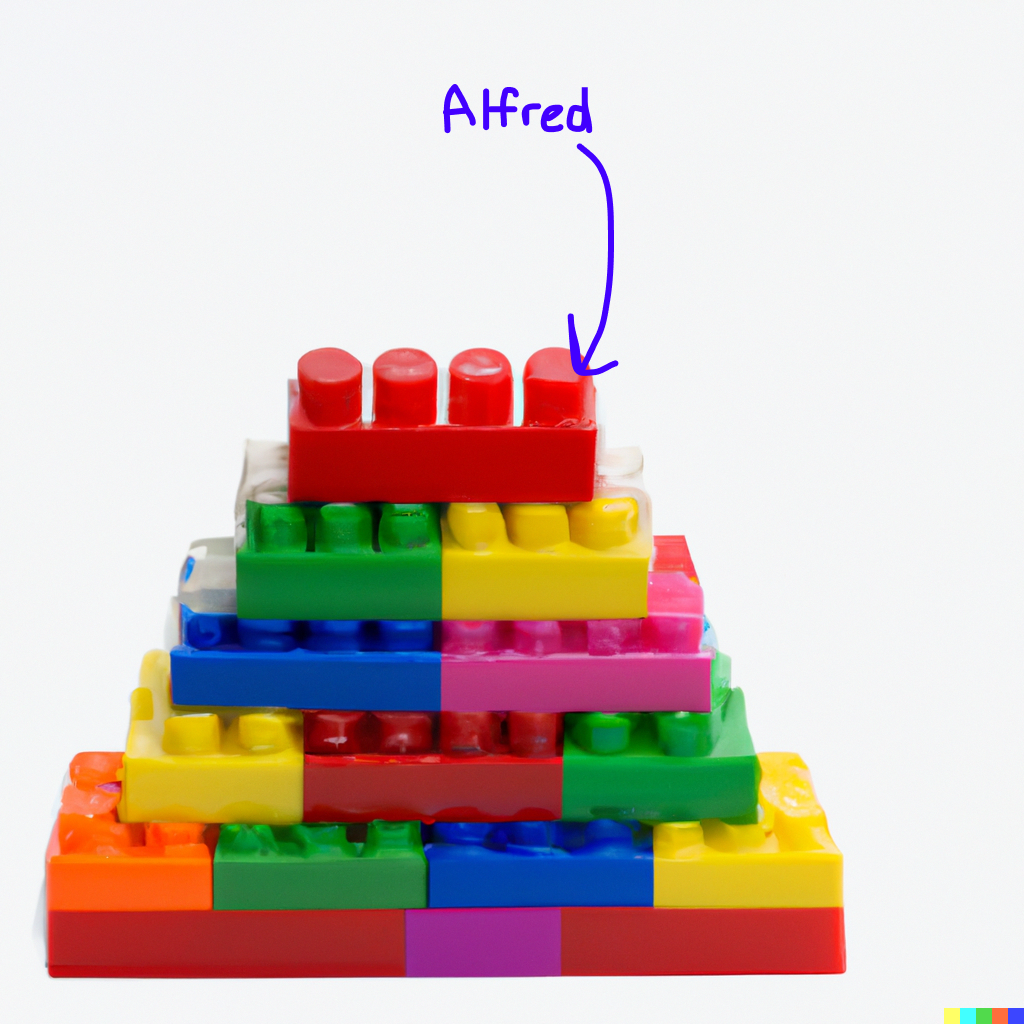Never mind the fact that this is a completely different set of lego blocks…

When the lego blogs are in this rigid shape, they have a more ordered relationship to each other than they did when they were floating about in the bowl. When we keep track of one piece of the pyramid and use that to keep track of the other pieces, the one piece can be described as an abstraction that somehow stands in for the rest of the blocks. At least, that’s what I think S is saying.

We live in a correlated world, where information about one object can give us information about other objects nearby. We can compress reality, because reality has order to it. Abstractions simply are those entities that, by virtue of the order in the world, can give us a lot of information. An abstraction can only exist in a world that has order, where entropy is not maximized.

So back to the simple problem: does the number 4 exist? I mean…yea? Each physical instance of four things is the number 4. Not eternally of course, only to the extent that this particular physical instantiation remains in place. To the extent that, in the course of its interactions with a constantly changing world, its “four-ness” is preserved, the number four is still there.

The symbol “4” is also where the number 4 can be found, to the extent that people in the world who interact with it recognize it as a number. If you have a muffin at Starbucks with a $4 price tag on it, people who walk in and out of the Starbucks will recognize that the muffin is worth four dollars, and if they want to pay in cash, they will take out four $1 bills from their pocket, or if they want to pay by credit, the computer will subtract four from their account balance. In a billion years, when no one has remembered english and all of society has fallen apart but somehow that $4 price tag has survived, it no longer refers to the number four, because it is no longer causally coupled with the world in such a a way as to preserve its “four-ness”.

(Before I continue, let me pause here and say: I’m kind of experimenting here, I’m not sure if any of this actually makes sense in the slightest, but this feels like something worth toying with further.)

At the end of the day, all of language, all of the order in the world, all of causality, is just about the patterns in reality, the continual coupling that goes on everywhere. The coupling, the clumping. Things clump and couple into increasingly complex ways. Biology is about clumping and coupling, thought and language are about clumping and coupling. The coupling and clumping is real, and it’s also physical, and there is nothing “beyond” the clumping and coupling, in some other realm—we don’t really need that other realm for anything.

You could still argue that it’s all just atoms, if you’d like. Well, sure? But it’s clearly not an undifferentiated mass of atoms! There is some clumping, some pattern. Why not call that clumping “4”, or “circle”, or “justice”? And the abstractions with which we attempt to refer to the world are not arbitrary: if you tried calling something “4” when it’s actually five, people will get confused and nothing will make sense. Abstractions do meaningfully refer to real physical things in the world.

Maybe it’s a very straightforward position to say: what “actually exists” is just this physical world around us…trees, flowers, chairs, humans, cells, atoms.² Within the space of things that exist, there is order, or pattern, as David Chapman puts it. Abstraction is just a way of referring to patterns in reality—in particular, a kind of compression. Abstractions are a way of chunking reality into causally significant regions.

Consider Ralph:

Ralph

Does Ralph exist? To the extent that we continue to perceive him, and engage with him, and talk about him, Ralph does exist. Once we turn off our computers and stop sharing dank memes on the internet, Ralph no longer exists. When I say “Ralph exists”, I’m not positing the existence of any special entity or substance outside the physical world. (And obviously not positing the existence of subjective feelings.) I’m literally referring to the existence of that picture, made up of pixels, ultimately generated by transistors and capacitors (or whatever computers are made of). That is a collection of pixels and transistors, and also, it is Ralph!

A few additional considerations below:

Are there problems with referring to abstractions as physical?

So, let’s admit, something feels weird about saying that when there are 4 chickens in the coop, they are, together, literally the number 4. (In addition to being a bunch of chickens, and being a bunch of atoms, and being a bunch of DNA strands, and so on.) It seems like we’ve lost something useful there: the distinction between an abstract entity and physical instantiations of that entity.

It’s nice to be able to say: there’s this abstract thing called the number 4, and that abstract thing is instantiated in a bunch of places in the physical world. And when those instantiations disappear, that number is still out there. By saying the abstraction is nothing more than a physical instantiation, I wonder if we lose something. Maybe we run into problems like: if there are two different chicken coops with 4 chickens each, are those two coops both instantiations of the same thing? Well, if the abstraction is physical, then…no?

Perhaps this is actually not a problem: we have two chicken coops, and they each have 4 chickens. The coops mirror each other in some capacity. But there isn’t some separate entity that they are both instantiations of. We don’t need that separate entity!

Are we really just taking the anti-4 position in slightly different terms?

Yes, I think we are. Anti-4’s claim that only physical things exist, and we agree. Where we differ from anti-4’s though is that we think it’s totally valid to point at a high-level entity (i.e. something larger than an atom) and say that it exists. So, we are not ontological reductionists.

What about irrational, complex, or cardinal numbers?

I guess they don’t exist. There are approximations to pi all over the world, but pi itself is never there. And as much as critical rationalists will hate this, perhaps this is a reasonable position. Same thing with i, infinity, and so on.

This doesn’t mean that talking about abstractions like pi or i is uninteresting or unhelpful, quite the contrary. They are still useful because the world does instantiate approximations of them. Also, we don’t understand the physical world that well: maybe pi really is instantiated in a bunch of places, perhaps at a scale much smaller than anything we’ve observed so far. Maybe there is an infinite number of something in the physical world.

Reframing “downward causation”

A lot of the time that people talk about reductionism and the existence of abstractions, they talk about the problem of “downward causation”. Do higher-level, emergent entities like humans have causal influence on lower-level entities like atoms? Are humans genuinely able to push stuff around in a way that is over and above the atoms themselves pushing things around?

I wonder if this formulation of abstractions as physical entities gets us closer to solving this problem. Consider: the problem of downward causality is one of whether some object A can have a causal influence on object B, e.g. by “pushing” it. But this actually assumes that causality itself generally takes the form of “A pushing B”. Something I liked about Popper’s writing was that he framed causality in a slightly different way.

Claims to causality are actually not generally in the form of “A pushing B”, but rather in the form “there is some regularity in the world in which A and B move in a particular way with respect to each other”. The important piece is the regularity, or the universal law, and not whether A is doing the “pushing” or if actually, B is doing the “pulling”. (I recommend reading my post for more details.) We mistakenly tend to think of causality kind of the way we think of logical implication, A ⇒ B, except instead of abstract propositions they’re actually objects, and that just doesn’t make sense.

If we stop thinking of causality as requiring some causally efficacious entity “pushing around” some non-causal entity that’s just being pushed around…then downward causality just doesn’t seem like a problem? It’s all just a matter of regularities in the world. There’s clumping and coupling, and things move in certain predictable ways. When I grab a cup of water from my table, it’s silly to ask “am I having a causal effect on the atoms in the cup”—everything is just in motion according to a set of patterns.

(Sidenote: Erik Hoel seems to have done some rigorous work on this, and reading that work is quite high on my todo list. I will report back if it provides a good answer to the questions I’m having.)

Addendum: maybe all this philosophizing is Bad, Actually?

David Chapman has gone on many times about how philosophy is a waste of time:

.@slatestarcodex vs. philosophy

[philosophy is bad. don’t do it. gently ridicule anyone who takes it seriously] https://t.co/fN9YpRlo8M pic.twitter.com/3qEChyezOX

— David Chapman (@Meaningness) August 23, 2022

When I first heard him talking about this, I was annoyed. I was very bought into the idea—absorbed from reading Popper and Deutsch—that philosophy is Great, as long as you do it Right. (David Deutsch, in The Beginning of Infinity, has a whole chapter on “Bad Philosophy”, which he defines as “philosophy that is not merely false, but actively prevents the growth of other knowledge”, unlike “good” philosophy.) Take Popper also:

it is a fact that purely metaphysical ideas—and therefore philosophical ideas—have been of the greatest importance for cosmology [i.e. science]. From Thales to Einstein, from ancient atomism to Descartes’s speculation about matter, from the speculations of Gilbert and Newton and Leibniz and Boscovic about forces to those of Faraday and Einstein about fields of forces, metaphysical ideas have shown the way.

The Logic of Scientific Discovery, page xxiii

But the more I’ve read of Chapman, the more I’ve come around to his view. What might he mean? Basically, it’s very easy to spend a long time going back and forth on debates about whether “abstractions really exist”, and end up with…nothing of note. A lot of these disagreements really might be, as Wittgenstein put it, quibbles over the meanings of words.

That said, I’m not ready to totally ready to give up philosophy, for three reasons: (1) maybe Chapman and Wittgenstein are wrong and there are interesting, important philosophical problems to solve; (2) thinking about these things can be fun; (3) beyond the utility of philosophy itself, there is a utility in trying to think about things in various ways and sussing out different arguments and definitions and so on, merely to exercise your brain’s thinking muscles. I really think I’ve gotten better at having productive intellectual conversations as a result of doing “philosophy”-like things: reading Popper, reading Deutsch, reading Chapman, writing blog posts about objective morality, and so on.

I’d like to think of my intellectual investments as a diversified portfolio—always spend some fraction of time thinking and reading about philosophy (it can be as little as 5% or 1%), but not all of your time. More than zero, but much less than the majority.